多摩美 – メディア芸術演習 VI – メディア・アート II 2014
第4回: openFrameworks基本 – 動きを極める、アニメーションのための様々なアルゴリズム
今回は、前回の内容をさらに発展させて、動きを生みだすための様々な手法について、サンプルを参照しながら解説していきます。
扱う動きは、実際に自然界に存在する様々な現象をシミュレーションします。以下のような内容を取り上げます。
- 引力、反発力
- 万有引力
- ばね、弾力
こうした様々な動きを生みだすアルゴリズムを理解することで、作品の表現力が格段に高まります。徐々に難易度が増してきましたが、ステップバイステップで、少しずつ理解していきましょう!
前回までの内容
前回は、動きを生みだす3つのベクトル(ofVec2f)を使用しました。
- 位置ベクトル
- 速度ベクトル
- 力ベクトル
これらのベクトルとくみあわせて、動き、摩擦、重力などを表現しました。それらの動きを1つにまとめてParticleと名付けて再利用可能なクラスとして独立させました。
Particleクラス
今回は、このParticleクラスをさらに発展させていきます。
引力、反発力
引力(Attraction Force)と、反発力(Repulsion Force)について考えます。
今回は、2次元の平面上での引力と反発力を扱います。ある一点を指定して、その一点に向かって平面上に引き付ける力(引力)と、ある一点から外に向けて反発する力(反発力)を設定します。全ての方面へ同じ力がかかる場合、力の中心から円形に力が働くようになります。また、中心点の距離が近ければ近いほど、大きな力が働くことになります。
この力をParticleのクラスのメソッド(クラスの関数)として実装します。いろいろな実装方法がありますが、今回は以下のように作成してみました。
引き付けあう力を加える – addAttractionForce
// 引き付けあう力
void Particle::addAttractionForce(float x, float y, float radius, float scale){
// 力の中心点を設定
ofVec2f posOfForce;
posOfForce.set(x,y);
// パーティクルと力の中心点との距離を計算
ofVec2f diff = position - posOfForce;
float length = diff.length();
// 力が働く範囲かどうか判定する変数
bool bAmCloseEnough = true;
// もし設定した半径より外側だったら、計算しない
if (radius > 0){
if (length > radius){
bAmCloseEnough = false;
}
}
// 設定した半径の内側だったら
if (bAmCloseEnough == true){
// 距離から点にかかる力ベクトルを計算
float pct = 1 - (length / radius);
diff.normalize();
force.x = force.x - diff.x * scale * pct;
force.y = force.y - diff.y * scale * pct;
}
}
反発する力を加える – addRepulsionForce
// 反発する力
void Particle::addRepulsionForce(float x, float y, float radius, float scale){
// 力の中心点を設定
ofVec2f posOfForce;
posOfForce.set(x,y);
// パーティクルと力の中心点との距離を計算
ofVec2f diff = position - posOfForce;
float length = diff.length();
// 力が働く範囲かどうか判定する変数
bool bAmCloseEnough = true;
// もし設定した半径より外側だったら、計算しない
if (radius > 0){
if (length > radius){
bAmCloseEnough = false;
}
}
// 設定した半径の内側だったら
if (bAmCloseEnough == true){
// 距離から点にかかる力ベクトルを計算
float pct = 1 - (length / radius);
diff.normalize();
force.x = force.x + diff.x * scale * pct;
force.y = force.y + diff.y * scale * pct;
}
}
これらのメソッドを加えて、Particleクラスを拡張します。
引力のサンプル1 – クリックした点に引き付ける力
引力と反発力を加味したパーティクルを平面上にランダムに配置して、マウスをクリックするとその点に引き付けられる(引力)がはたらくようにしてみます。大量の点の描画は、前回にも使用したVBO Meshを使用して高速化を計ります。
パーティクルにかかる引力は、testApp::update()で計算します。以下のようにしてみました。
void ofApp::update(){
// パーティクルの数だけ計算
for (int i = 0; i < particles.size(); i++){
// 力をリセット
particles[i].resetForce();
// もし引力がはたらいていたら
if (atraction) {
// マウスの位置に引力を加える
particles[i].addAttractionForce(mouseX, mouseY, ofGetWidth(), 0.1);
}
// パーティクル更新
particles[i].update();
// 画面の端にきたら反対側へ
particles[i].throughOfWalls();
}
}
空間内に引力が働き、複雑な動きとパターンが生まれます。
Experiment of Attraction from Atsushi Tadokoro on Vimeo.
引力のサンプル2 – 万有引力
では、次に、全てのパーティクル同士で引力がはたらくようにしてみましょう。つまり、「全ての質点(物体)は互いに gravitation(=引き寄せる作用、引力、重力)を及ぼしあっている」という万有引力の法則を実装してみます。
- 参考: Wikipedia – 万有引力
このために、引力と反発力のための関数、addAttractionForceとaddRepulsionForceに、もうひとつバリエーションを増やします。新たなバージョンは力の中心点にベクトル(ofVec2f)ではなくパーティクルのオブジェクトParticleを参照できるようにします。
引き付けあう力Particle版 – addAttractionForce
void Particle::addAttractionForce(Particle &p, float radius, float scale){
// 力の中心点を設定
ofVec2f posOfForce;
// Particleへの参照から座標を取得、力の中心に設定
posOfForce.set(p.position.x, p.position.y);
// パーティクルと力の中心点との距離を計算
ofVec2f diff = position - posOfForce;
float length = diff.length();
// 力が働く範囲かどうか判定する変数
bool bAmCloseEnough = true;
// もし設定した半径より外側だったら、計算しない
if (radius > 0){
if (length > radius){
bAmCloseEnough = false;
}
}
// 設定した半径の内側だったら
if (bAmCloseEnough == true){
// 距離から点にかかる力ベクトルを計算
float pct = 1 - (length / radius);
diff.normalize();
force.x = force.x - diff.x * scale * pct;
force.y = force.y - diff.y * scale * pct;
// 参照したパーティクルの力を計算して更新
p.force.x = p.force.x + diff.x * scale * pct;
p.force.y = p.force.y + diff.y * scale * pct;
}
}
反発する力Particle版 – addRepulsionForce
void Particle::addRepulsionForce(Particle &p, float radius, float scale){
// 力の中心点を設定
ofVec2f posOfForce;
// Particleへの参照から座標を取得、力の中心に設定
posOfForce.set(p.position.x,p.position.y);
// パーティクルと力の中心点との距離を計算
ofVec2f diff = position - posOfForce;
float length = diff.length();
// 力が働く範囲かどうか判定する変数
bool bAmCloseEnough = true;
// もし設定した半径より外側だったら、計算しない
if (radius > 0){
if (length > radius){
bAmCloseEnough = false;
}
}
// 設定した半径の内側だったら
if (bAmCloseEnough == true){
// 距離から点にかかる力ベクトルを計算
float pct = 1 - (length / radius);
diff.normalize();
force.x = force.x + diff.x * scale * pct;
force.y = force.y + diff.y * scale * pct;
// 参照したパーティクルの力を計算して更新
p.force.x = p.force.x - diff.x * scale * pct;
p.force.y = p.force.y - diff.y * scale * pct;
}
}
このメソッドをofAppで活用します。生成したパーティクルの全ての間で引力を設定するには、以下のようにupdate()内で、for文を二重にして全ての組み合わせについて計算していきます。
ofApp::update()
void ofApp::update(){
for (int i = 0; i < particles.size(); i++){
// 力をリセット
particles[i].resetForce();
// パーティクル同士の反発する力
for (int j = 0; j < i; j++){
particles[i].addAttractionForce(particles[j], 120.0, 0.001);
}
// マウスをクリックした点に引力を加える
if (atraction) {
particles[i].addAttractionForce(mouseX, mouseY, ofGetWidth(), 0.1);
}
// 力と位置の更新
particles[i].update();
// 壁の端にきたら、反対側へ
particles[i].throughOfWalls();
}
}
この内容を実装します。
万有引力が実現できました。徐々にお互いが引き付けあうグループが生まれます。
Experiment of Attraction 2 from Atsushi Tadokoro on Vimeo.
引力のサンプル3 – 質量を加味した万有引力
万有引力の強さは、距離だけでなく物体の質量によって強さが変化します。
万有引力の大きさFは、物体の質量を M,m 、物体間の距離を r とすると、以下の式が成立します。Gは万有引力定数と呼ばれる比例定数です。
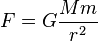
つまり、力の大きさは、物体同士の質量の積(かけ算)を距離の二乗で割った値に比例するということです。
この質量による力の変化を加味して、さらに万有引力を拡張してみましょう。それぞのParticleクラスに質量(mass)というプロパティーを追加して、このmassの値によって、力を変化させてみます。testApp::update() を以下のように更新しました。
void ofApp::update(){
for (int i = 0; i < particles.size(); i++){
particles[i].resetForce();
// パーティクル同士の引き付けあう力
for (int j = 0; j < i; j++){
// 引力の強さは、2つの物体の質量の積に比例する
float strength = particles[j].mass * particles[i].mass * 0.001;
// 質量を加味した力を引力に加える
particles[i].addAttractionForce(particles[j], 200, strength);
}
particles[i].update();
particles[i].throughOfWalls();
}
}
この内容を加えてプログラムを更新します。
さらにリアルな世界になりました。混沌から銀河が生成されるようにも感じられます。
Experiment of Attraction 3 from Atsushi Tadokoro on Vimeo.
ばねの力(弾力)
次に、ばねにかかる力(弾力)について考えてみます。ばねに働く力に関する計算は、フックの法則によって求まります。この式のFは力、Xはばねの長さ、kは「ばね定数」と呼ばればね固有の強さを表しています。

この式の解釈は簡単です。つまり、ばねは伸びた長さに比例して力が発生するということです。

この法則を利用して、ばねの動きを生みだしていきましょう。
今回は、ばねの両端にはParticleがあり、この2つのParticleを接続するばねSpringがあると考えます。
2つのParticleオブジェクトにかかる力から位置を更新します。この力を計算するために、Springという新たなクラスを作成しました。
Spring.h
#pragma once
#include "ofMain.h"
#include "Particle.h"
class Spring {
public:
// コンストラクタ
Spring();
// 両端のParticleへの参照
Particle *particleA;
Particle *particleB;
// 力をかけていない状態のばねの長さ
float distance;
// ばね定数
float springiness;
void update();
void draw();
};
Spring.cpp
#include "Spring.h"
//---------------------------------------------------------------------
Spring::Spring(){
// 初期化、最初はばねを空(NULL)に
particleA = NULL;
particleB = NULL;
}
//---------------------------------------------------------------------
void Spring::update(){
// もし両端にParticleが設定されていない場合、何もしない
if ((particleA == NULL) || (particleB == NULL)){
return;
}
// 両端のParticleの位置を取得
ofVec2f pta = particleA->position;
ofVec2f ptb = particleB->position;
// 距離を算出
float theirDistance = (pta - ptb).length();
// 距離からばねにかかる力を計算(フックの法則)
float springForce = (springiness * (distance - theirDistance));
// ばねの力から、両端への力ベクトルを計算
ofVec2f frcToAdd = (pta-ptb).normalized() * springForce;
// それぞれのParticleに力を加える
particleA->addForce(ofVec2f(frcToAdd.x, frcToAdd.y));
particleB->addForce(ofVec2f(-frcToAdd.x, -frcToAdd.y));
}
//---------------------------------------------------------------------
void Spring::draw(){
// もし両端にParticleが設定されていない場合、何もしない
if ((particleA == NULL) || (particleB == NULL)){
return;
}
// ばねを描画
ofLine(particleA->position.x, particleA->position.y, particleB->position.x, particleB->position.y);
}
ばね サンプル1 – 単体のばね
では、このクラスを利用して、ばねを作成してみましょう。Particleクラスはそのまま利用します。
空間にバネが表示されます。マウスをドラッグすると、ばねの片方の端を移動可能です。
ばね サンプル2 – ばねの連結
では、次にばねをどんどん連結してみましょう。SpringクラスとParticleクラスが既に作成されているので、とても簡単に応用可能です。連結数は最大数を変更できるよう、それぞれvector(可変長配列)として用意します。
SpringクラスとParticleクラスはそのまま利用して、ofAppのみを変更します。
Spring 1 from Atsushi Tadokoro on Vimeo.
ばね サンプル3 – ばねと引力・反発力
せっかくParticleに引力と反発力を実装しているので、これとばねを組合せてみたいと思います。ばねを連結して、それぞれのPartile同士に反発力を生成します。すると、どのような動きになるでしょうか? さらにここではマウスをクリックするとそれぞれのParticleに対する引力、クリックしていない場合には反発力として作用するようにしています。
今回もofAppのみの変更です。
弾力をもった、ひとつの物体のようになりました。ばね定数(springness)や、Particle同士の反発力を調整することで、様々な表情をコントロール可能です。
Spring 2 from Atsushi Tadokoro on Vimeo.
また、描画の際にParticleをSpringを描くのではなく、輪郭をひとつの線分として描き内部を塗ることで、さらに面白い効果が生まれます。
Spring 3 from Atsushi Tadokoro on Vimeo.
本日はここまで!